共计 6276 个字符,预计需要花费 16 分钟才能阅读完成。
AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
本篇工作已被NeurIPS(2024 Conference on Neural Information Processing Systems)会议接收,文章第一作者为美国埃默里大学的博士生白光霁,通讯作者为赵亮教授,来自埃默里大学计算机系。共同作者包括美国阿贡国家实验室的Yijiang Li和Kibaek Kim,以及埃默里大学的博士生凌辰。该研究主要探讨了大语言模型的全局剪枝方法,旨在提高预训练语言模型的效率。该成果的发表为大模型的剪枝与优化研究提供了新的视角,并在相关领域具有重要的应用潜力。

情景导入
随着大型语言模型(LLMs)如 GPT 和 LLaMA 在自然语言处理领域的突破,现如今的模型能够在各种复杂的语言任务中表现优异。然而,这些模型往往包含数十亿参数,导致计算资源的需求极为庞大。为了让LLMs在更多的实际应用中变得可行,研究人员进行了大量的模型压缩工作,其中包括剪枝、量化、知识蒸馏和低秩分解等方法。
剪枝作为一种重要的压缩策略,通过引入稀疏性提升了内存和计算效率。尽管剪枝的有效性已在视觉任务和较小规模的语言模型中得到验证,但全局剪枝由于需要将整个模型加载到同一个GPU中,对于如今的大规模LLMs而言是不现实的。因此,近年来出现了局部剪枝方法比如SparseGPT和Wanda,尽管这些方法简单粗暴地局部化每个layer的剪枝,从而在效率上有了提升,但局部剪枝带来的效果往往是次优 (suboptimal) 的。
我们提出的 SparseLLM 框架,通过将全局剪枝问题分解为更易管理的子问题,从而在高稀疏度下也能实现高效的优化和优异的性能。SparseLLM 在实现了内存和计算效率的同时,超越了当前最先进的剪枝方法,为LLMs的压缩和应用树立了新的标杆。
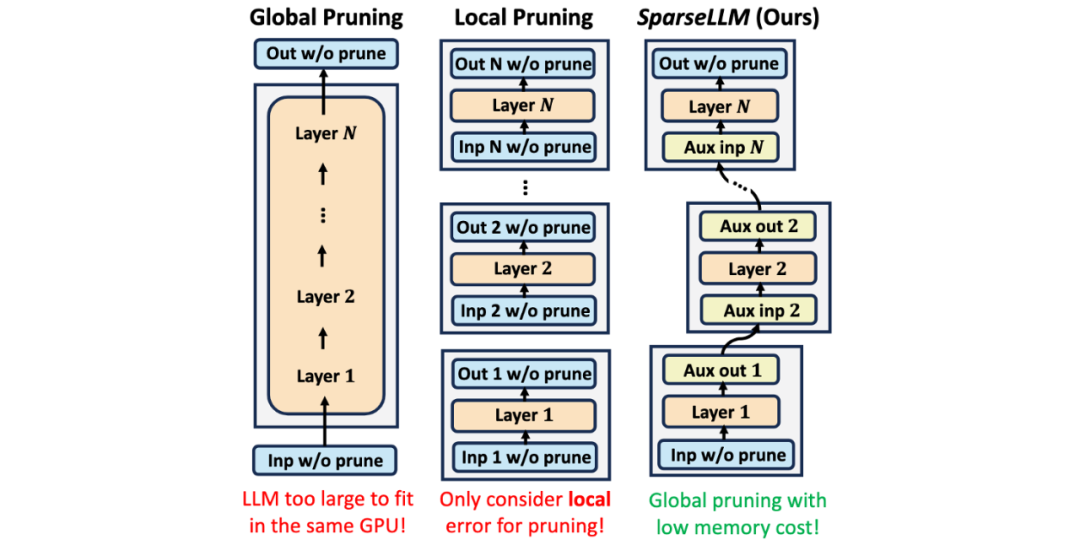
Figure 1: 此图展示了全局剪枝、局部剪枝与我们提出的 SparseLLM 框架的对比。全局剪枝(左):由于需要将整个模型加载到同一GPU中,内存消耗过大,难以适用于大规模LLMs。局部剪枝(中):只考虑每一层的局部误差,尽管内存需求较低,但会导致次优的全局性能。SparseLLM(右):通过引入辅助输入和输出,将全局剪枝问题分解为可管理的子问题,实现低内存开销下的全局剪枝,保持全局最优性能。
现有方法及其缺陷
在模型剪枝中,剪枝方法主要分为两大类:全局剪枝(Global Pruning)和局部剪枝(Local Pruning)。
全局剪枝
全局剪枝旨在对整个模型应用统一的稀疏化掩码(sparsity mask),以最小化未压缩模型与压缩模型之间的全局损失。虽然理论上全局剪枝可以为模型提供最优的性能,尤其是在高稀疏度情况下,但它的主要缺点在于其内存开销巨大。为了实现全局剪枝,整个模型必须被加载到同一个GPU中,这对于如今规模巨大的LLMs(如GPT和LLaMA)来说是不现实的。
局部剪枝
为了规避全局剪枝的内存瓶颈,局部剪枝通过将模型压缩分解为每一层的子问题来减少内存消耗。局部剪枝的方法通常会对每一层的输出进行独立的稀疏化,并构造局部损失来衡量未压缩和压缩层之间的差异。虽然局部剪枝方法在资源使用方面更加高效,但由于它只关注每一层的局部最优解,导致了全局上次优的模型性能,尤其是在高稀疏度下表现尤为显著。
方法缺陷
局部剪枝的局限性在于它无法很好地捕捉模型层之间的相互依赖关系,只针对各层的稀疏化进行优化。这种过度约束每层激活值的行为,容易导致全局性能的下降。因此,尽管局部剪枝在某些情况下能带来效率提升,但它往往无法达到全局剪枝所能带来的最优性能。
技术方法
在SparseLLM框架中,我们的目标是实现全局剪枝。SparseLLM通过将全局剪枝目标分解为多个子问题,每个子问题可以使用较少的资源解决,并且可以协同实现全局剪枝目标。SparseLLM的优势在于它能够在内存消耗较低的情况下实现全局剪枝。
动机
SparseLLM的开发基于以下观察:LLMs可以被表述为一个复合函数,后一个模块的输出是下一个模块的输入。这使得可以通过辅助变量将全局剪枝目标重新表述为等价形式,从而将其分解为多个子问题。然后,开发了一种高效的算法,通过交替优化每个子问题来实现全局最优解。
剪枝问题的重新表述
我们通过对模型的稠密线性部分和非线性部分进行解耦,重新表述了剪枝问题。将每一层的输出存储为一个新变量 ,非线性层的输出则表示为激活值 。接着,我们优化以下目标函数:
其中约束条件为:
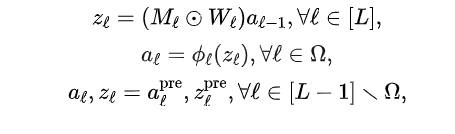
这里
表示模型的总层数,
表示需要剪枝的层集合,
和
分别代表原始预训练模型的中间变量值。 是模型的最终输出结果 。
Remark:
这个公式具有高度的通用性和灵活性。当
时,解决该问题等同于全局剪枝。而当
时,问题简化为局部剪枝,独立地考虑每一层。通过调节
的大小,我们可以在全局和局部剪枝之间无缝切换。
SparseLLM优化过程
原始的全局剪枝问题包含全局约束条件,为了避免直接求解带约束的目标函数,我们引入了辅助变量和惩罚函数。通过引入
惩罚项,原始的全局目标函数被转化为无约束问题,具体表达如下:
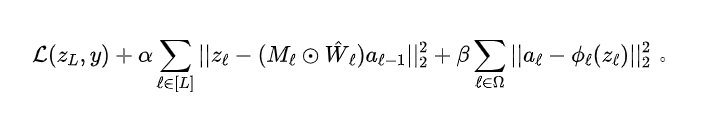
其中,
和
是超参数。这样,我们将每一层的剪枝问题解耦为局部子问题,同时保留了层之间的依赖性。
SparseLLM算法的关键在于上面公式中的的灵活性,目的是在完全全局剪枝(会导致内存瓶颈)和完全局部剪枝(会导致次优性能)之间找到更好的折中。粗暴地对所有层进行全局剪枝是不现实的。最近的研究表明,前馈网络 (FFN) 模块在每个解码器层中的参数占LLM总参数的三分之二以上。因此,SparseLLM优先对FFN模块进行全局剪枝,同时仍然遵循对多头注意力模块 (MHA) 的局部剪枝策略(见Figure 2)。这种策略在剪枝大规模模型的计算可行性与剪枝过程的有效性之间取得了平衡,并遵循了现有LLM剪枝框架的限制和实践。
具体而言,SparseLLM将
设置为
,其中
表示每个解码器层FFN模块中线性层的索引集(具体数学细节详见论文)。也就是说,同一个FFN模块中的线性层被全局剪枝,而剩下的线性层仍按照局部剪枝。对于每一层的FFN模块,我们的目标是最小化以下无约束的目标函数:
此时,每一层的剪枝问题被表述为线性投影模块(上投影和下投影)的优化问题,并且可以针对每一个子问题进行交替优化。这一过程通过引入辅助变量和惩罚函数,使得我们能够在不消耗过多内存的前提下,求解全局最优解。
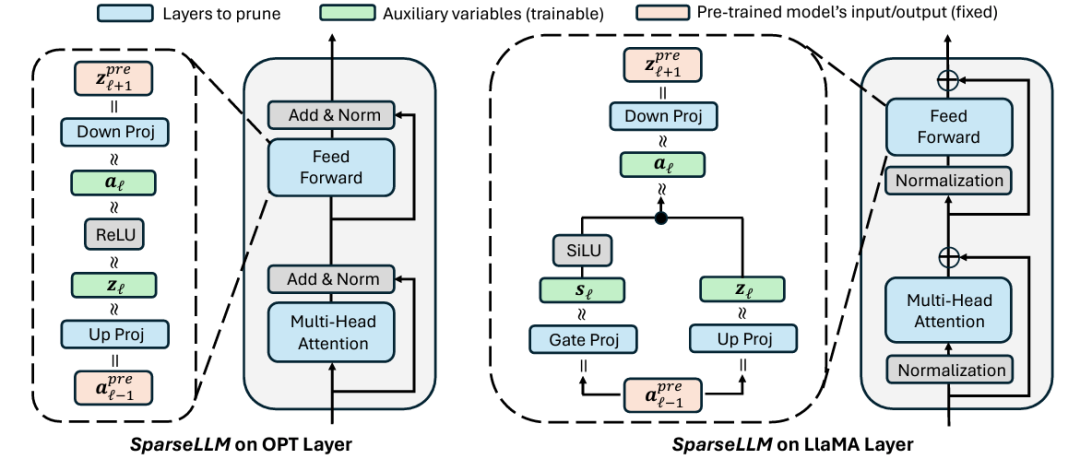
Figure 2: 该图展示了 SparseLLM 框架在不同LLM架构中的工作原理。左侧描绘了在 OPT模型中的剪枝流程。SparseLLM通过引入辅助变量,将全局剪枝问题分解为可管理的子问题,利用线性层的上下投影模块(Up Proj 和 Down Proj)以及ReLU激活函数来实现模型压缩。右侧描绘了在 LLaMA模型 中的剪枝流程。此处,SparseLLM除了使用线性层的上下投影外,还利用了SiLU激活函数与Gate Proj模块来实现更复杂的剪枝操作。图中标注了剪枝层(蓝色)、辅助变量(绿色)和预训练模型的固定输入/输出(粉色),以帮助理解各模块在剪枝过程中的相互关系与作用。
OPT 模型中的子问题求解
在 OPT 模型中,我们的目标是对每一层的FFN模块进行全局剪枝。根据公式5,我们首先考虑交替优化子问题,对于每一个子问题的闭式解,我们分以下步骤进行:
剪枝权重的优化:首先,我们固定其他变量,优化权重
和
。具体来说,优化目标是最小化以下表达式:
为了求解该问题,我们首先对
进行分解:
,其中
( 表示伪逆)。通过将分解后的 带入原始损失函数中,可以得到权重剪枝问题的闭式解,类似于 SparseGPT 等剪枝方法。
激活值的更新:对于激活值
的优化,这是一个类似于权重剪枝的简单最小二乘问题。激活值
的更新可以通过如下公式求解:
输出的更新:对于输出
,我们最小化以下非凸的损失函数:
由于ReLU函数的逐元素操作,问题可以通过简单的if-then逻辑分为两种情况:
LLaMA 模型中的子问题求解
在LLaMA模型中,我们的剪枝过程与OPT模型类似,唯一不同的是LLaMA模型中包含额外的门控投影层,并使用了SiLU激活函数。我们针对LLaMA的各层子问题进行如下求解:
剪枝权重的优化:对于LLaMA模型中的FFN模块,权重剪枝的优化过程与OPT模型类似。我们通过最小化以下表达式来优化权重:
并使用类似于OPT模型的分解方法求解。
激活值的更新:在LLaMA模型中,我们使用SiLU激活函数,因此激活值的更新公式如下:
输出的更新:对于LLaMA模型中的输出
,我们最小化以下损失函数:
通过类似的数学操作,我们可以求得
的解析解为:
门控投影输出
的更新:对于门控投影层的 ,我们通过最小化以下表达式来更新:
由于SiLU函数的非凸特性,问题可以通过查找预先计算好的解决方案的查找表来快速求解。
通过上述过程,SparseLLM能够在LLaMA和OPT两种模型架构中实现高效的全局剪枝,最大化压缩效果的同时,保持模型的全局性能。
实验部分实验设置
为了验证SparseLLM 框架的有效性,我们在多个大规模语言模型上进行了广泛的实验。我们使用了 PyTorch 框架并结合 HuggingFace 的 Transformers 库来处理模型和数据集。所有剪枝实验均在 NVIDIA A100 GPU 上执行,以确保实验结果具备较好的可扩展性和适用性。
实验的数据集选取了 WikiText2 (WT2)、PTB(Penn Treebank),以及 C4 的验证集。这些数据集是语言模型压缩任务中的标准基准集,确保了结果的广泛适用性。为了保持公平性,我们在所有实验中使用了相同的数据子集,并确保剪枝过程为零样本设置,即不引入额外的训练数据,仅依赖于模型的预训练权重进行剪枝。
我们采用了模型的 困惑度(Perplexity) 作为评估指标,这是一种常用的衡量语言模型生成能力的指标。困惑度越低,模型的表现越好。所有剪枝后的模型均通过困惑度指标评估其在不同数据集上的性能,比较剪枝前后的性能变化以及不同稀疏度下的性能差异。
模型与剪枝策略
实验中,我们选择了两类主流的预训练语言模型进行剪枝实验:
对于每一个模型,我们使用了不同的稀疏度设定,从 70% 到 90% 的非结构化稀疏度,以及 3:4 的半结构化稀疏度。在每个稀疏度水平下,我们测试了模型在各个基准数据集上的性能表现,以验证 SparseLLM 在不同稀疏度条件下的剪枝效果。
比较基线方法
为了全面评估SparseLLM 的效果,我们与现有的几种剪枝方法进行了对比:
我们分别在不同稀疏度条件下与上述方法进行了对比,详细记录了各模型在不同数据集上的困惑度结果。
结果分析
在不同稀疏度条件下,SparseLLM 在大多数情况下能够显著超过基线方法,特别是在高稀疏度(≥ 70%)的情况下,SparseLLM 能够维持较低的困惑度,甚至在一些任务中超越了未剪枝的模型。相比之下,局部幅度剪枝方法和 SparseGPT 的性能在稀疏度较高时下降明显,证明了全局剪枝方法在模型压缩中的优势。
此外,我们还分析了模型剪枝后的参数分布情况。SparseLLM 的剪枝策略能够有效地保持模型重要参数的位置不变,减少了剪枝过程中重要信息的丢失,这也解释了其在高稀疏度下性能优越的原因。
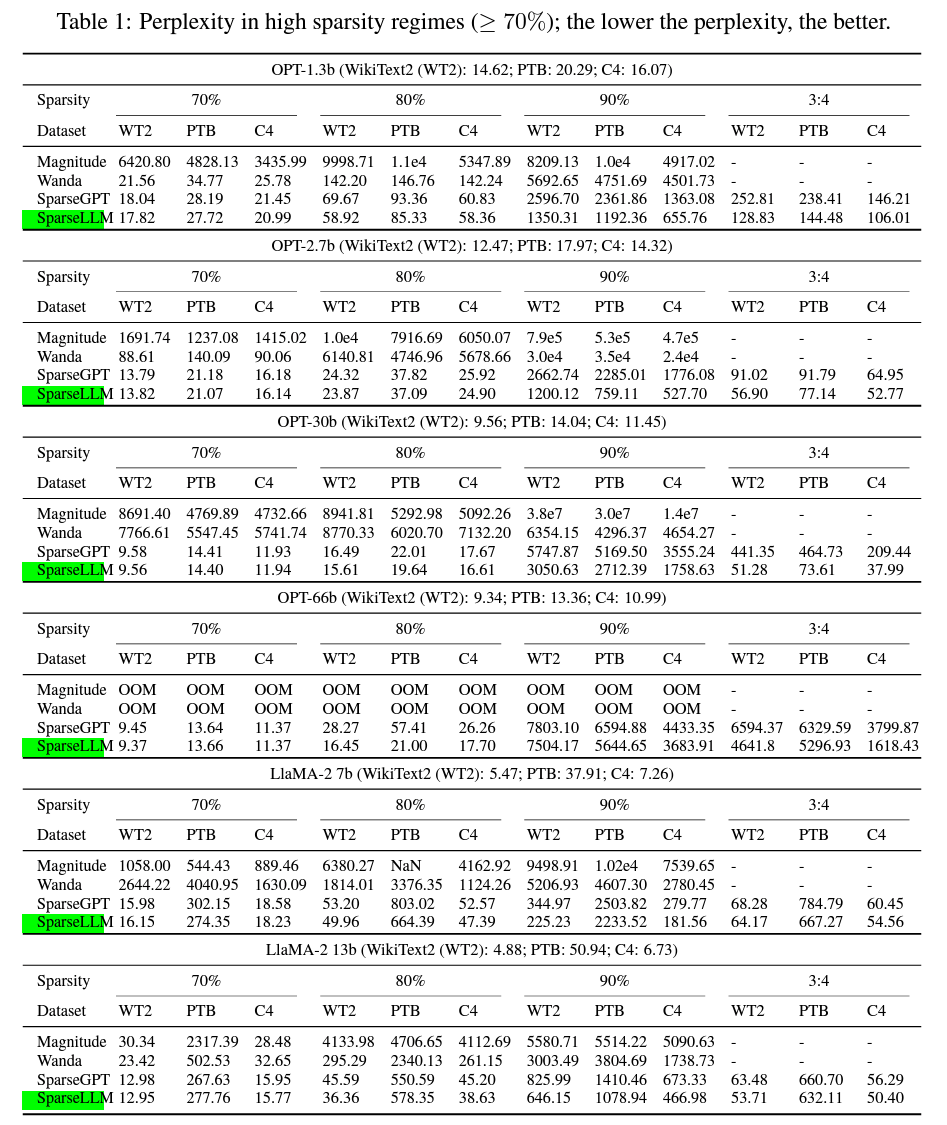
我们进一步分析了不同大小模型在使用 SparseLLM 剪枝时的表现。实验表明,较大规模的模型在剪枝后的性能更为稳定,尤其是 LLaMA 13b 等大规模模型,即使在90%稀疏度下,困惑度的增幅也非常有限。这一结果表明,随着模型规模的增加,SparseLLM 能够更有效地在剪枝中找到最优的权重保留策略,降低剪枝对模型性能的负面影响。
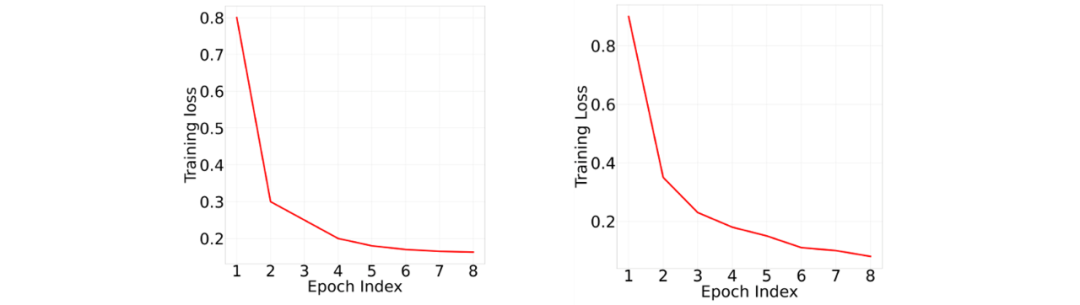
Figure 3: Fast convergence of SparseLLM. Training loss per epoch for pruning layer 3 of OPT-125m at 80% sparsity (Left) and layer 6 of LlaMA-2 13b at 70% sparsity (Right).
除了剪枝性能,我们还对 SparseLLM 的收敛速度进行了分析。在实际训练过程中,SparseLLM 在最初的几个 epoch 内即可快速达到较低的训练损失,表明其剪枝过程非常高效。相比之下,其他局部剪枝方法在稀疏度较高时,需要更多的训练步骤才能收敛到类似的性能水平。这进一步证明了全局剪枝策略在保持模型性能的同时,能够有效减少训练时间和资源消耗。
为了验证 SparseLLM 在零样本设置下的通用性,我们在多个零样本任务上测试了剪枝后的模型性能。实验结果表明,SparseLLM 在大多数任务上保持了优异的性能,特别是在涉及推理和生成任务时,SparseLLM 剪枝后的模型仍然能够生成高质量的文本输出,而其他基线方法的性能在高稀疏度下显著下降。
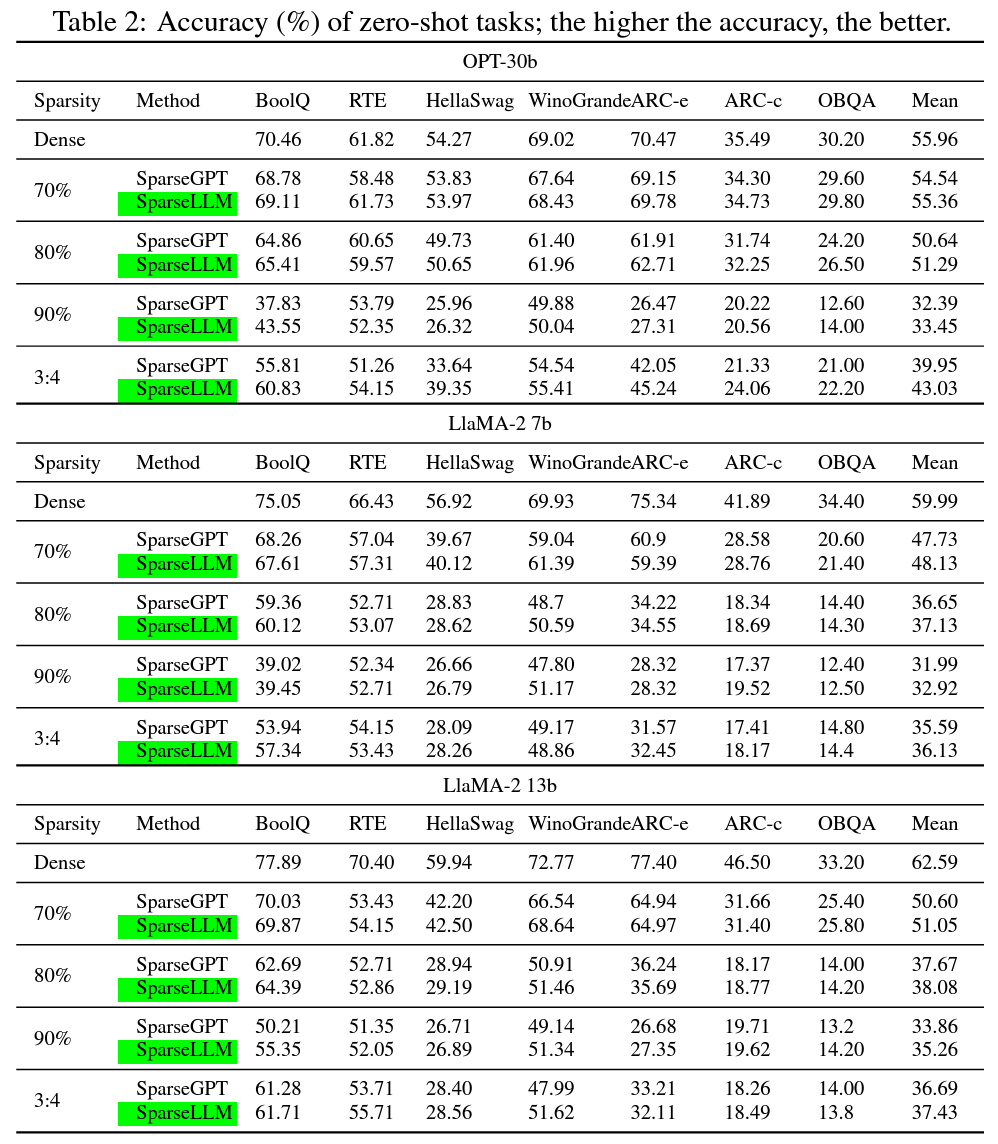
实验小结
实验结果表明,SparseLLM 框架能够在不同规模的预训练语言模型上实现高效的全局剪枝,同时保持良好的模型性能。无论是在较小的 OPT 模型上,还是在更大规模的 LLaMA 模型上,SparseLLM 均表现出色,特别是在高稀疏度的条件下表现尤为突出。此外,SparseLLM 的收敛速度和剪枝后的通用性也为其在实际应用中的高效性和适用性提供了强有力的支持。
结论
在本研究中,我们提出了SparseLLM,一个针对大规模预训练语言模型的全局剪枝框架。通过引入辅助变量和局部子问题,我们成功解决了全局剪枝在计算和内存方面的瓶颈。实验结果表明,SparseLLM 能够在保持模型性能的同时,在高稀疏度下有效地压缩模型。与现有的剪枝方法相比,SparseLLM 在困惑度、稀疏度和通用性方面展现出了显著的优势,特别是在处理大型模型(如 LLaMA 和 OPT 系列)时,SparseLLM 的全局剪枝策略展现了更好的性能保持能力。
通过本研究,我们证明了全局剪枝在大规模语言模型中的潜力,不仅能够显著降低模型的计算和存储成本,还能在高稀疏度下维持优异的性能。这为实际应用中对资源敏感的任务提供了一个有效的解决方案。
未来研究方向
虽然SparseLLM 取得了优异的结果,但仍有若干值得深入研究的方向:
动态剪枝策略的研究:当前的 SparseLLM 是基于静态的全局剪枝策略,即在训练前决定剪枝的层和稀疏度。未来可以探索动态剪枝策略,结合任务需求和模型训练过程,实时调整剪枝比例和剪枝区域,以进一步提升模型压缩效率。
稀疏性与硬件加速的结合:尽管 SparseLLM 能够大幅减少模型的计算和存储开销,但在实际部署中如何高效利用硬件加速器(如GPU、TPU)的稀疏性支持仍是一个开放问题。未来的工作可以研究如何更好地结合稀疏矩阵乘法和硬件加速技术,以实现更大的性能提升。
剪枝后的模型微调:尽管我们的实验已经展示了 SparseLLM 在高稀疏度下的性能保持能力,但剪枝后的模型是否可以通过微调进一步提升性能仍然值得探索。未来的研究可以结合剪枝和微调技术,探讨如何在稀疏化后进一步优化模型性能。
通过探索这些方向,SparseLLM 有望在大规模语言模型的压缩与高效推理中发挥更加广泛的作用,为各类NLP应用提供更多的支持与创新。





