共计 2850 个字符,预计需要花费 8 分钟才能阅读完成。
该方法不要求同一种算法只能对应一种结构,相反,该方法可以利用优化问题的等价表示设计更多的网络架构,体现其灵活性。例如,线性化交替方向乘子法通常用于求解约束优化问题:
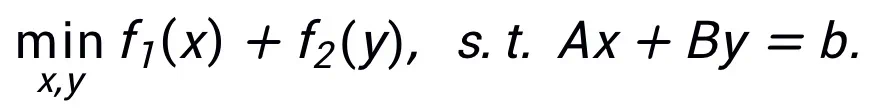
通过令
即可得到一种可启发网络的更新迭代格式:
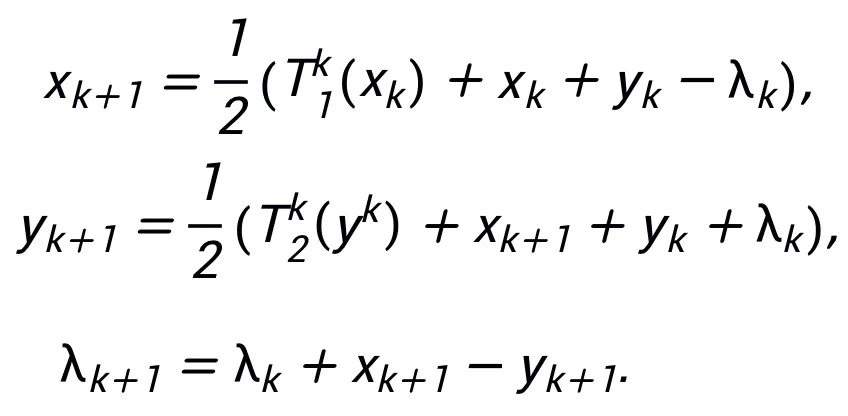
其启发的网络结构可见图 2。

图 2 线性化交替方向乘子法启发的网络结构
启发的网络具有万有逼近性质
对该方法设计的网络架构,可以证明,在模块满足此前条件以及优化算法(在一般情况下)稳定、收敛的条件下,任意一阶优化算法启发的神经网络在高维连续函数空间具有万有逼近性质,并给出了逼近速度。论文首次在有限宽度设定下证明了具有一般跨层连接的神经网络的万有逼近性质(此前研究基本集中在 FCNN 和 ResNet,见表 1),论文主定理可简略叙述如下:
主定理(简略版):设
A 是一个梯度型一阶优化算法。若算法 A 具有公式 (1) 中的更新格式,且满足收敛性条件(优化算法的常用步长选取均满足收敛性条件。若在启发网络中均为可学习的,则可以不需要该条件),则由算法启发的神经网络:
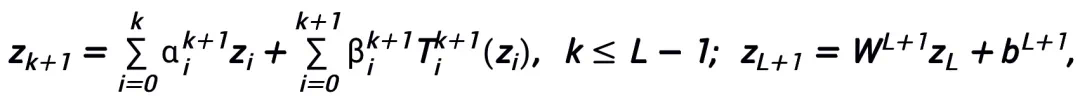
在连续(向量值)函数空间
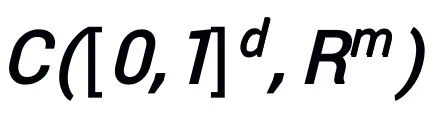
以及范数
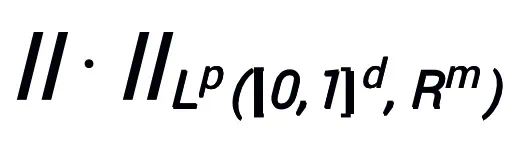
下具有万有逼近性质,其中可学习模块 T 只要有包含两层形如

的结构(σ 可以是常用的激活函数)作为其子结构都可以。
常用的 T 的结构如:
1)卷积网络中,pre-activation 块:BN-ReLU-Conv-BN-ReLU-Conv (z),
2)Transformer 中:Attn (z) + MLP (z+Attn (z)).
主定理的证明利用了 NODE 的万有逼近性质以及线性多步方法的收敛性质,核心是证明优化算法启发设计的网络结构恰对应一种收敛的线性多步方法对连续的 NODE 的离散化,从而启发的网络 “继承” 了 NODE 的逼近能力。在证明中,论文还给出了 NODE 逼近 d 维空间连续函数的逼近速度,解决了此前论文 [6] 的一个遗留问题。
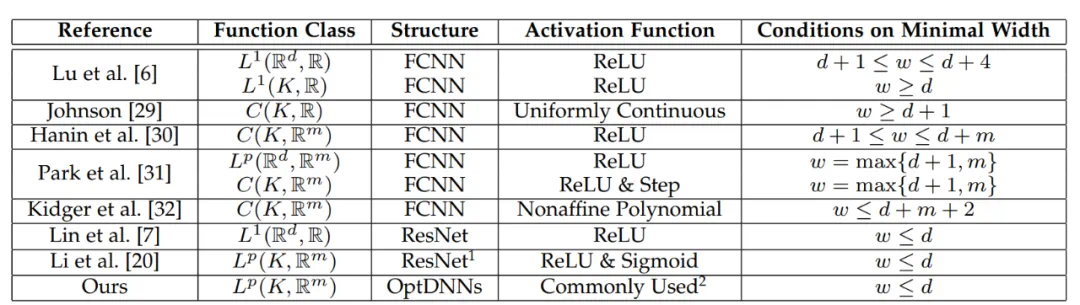
表 1 此前万有逼近性质的研究基本集中在 FCNN 和 ResNet
实验结果
论文利用所提出的网络架构设计框架设计了 8 种显式网络和 3 种隐式网络(称为 OptDNN),网络信息见表 2,并在嵌套环分离、函数逼近和图像分类等问题上进行了实验。论文还以 ResNet, DenseNet, ConvNext 以及 ViT 为 baseline,利用所提出的方法设计了改进的 OptDNN,并在图像分类的问题上进行实验,考虑准确率和 FLOPs 两个指标。
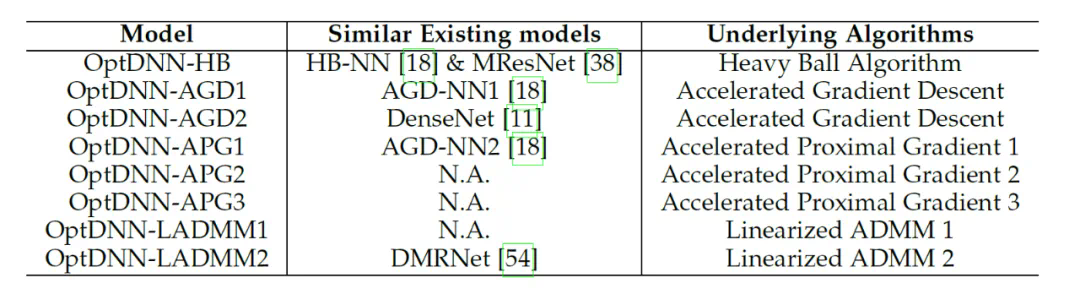
表 2 所设计网络的有关信息
首先,OptDNN 在嵌套环分离和函数逼近两个问题上进行实验,以验证其万有逼近性质。在函数逼近问题中,分别考虑了逼近 parity function 和 Talgarsky function,前者可表示为二分类问题,后者则是回归问题,这两个问题都是浅层网络难以逼近的问题。OptDNN 在嵌套环分离的实验结果如图 3 所示,在函数逼近的实验结果如图 3 所示,OptDNN 不仅取得了很好的分离 / 逼近结果,而且比作为 baseline 的 ResNet 取得了更大的分类间隔和更小的回归误差,足以验证 OptDNN 的万有逼近性质。
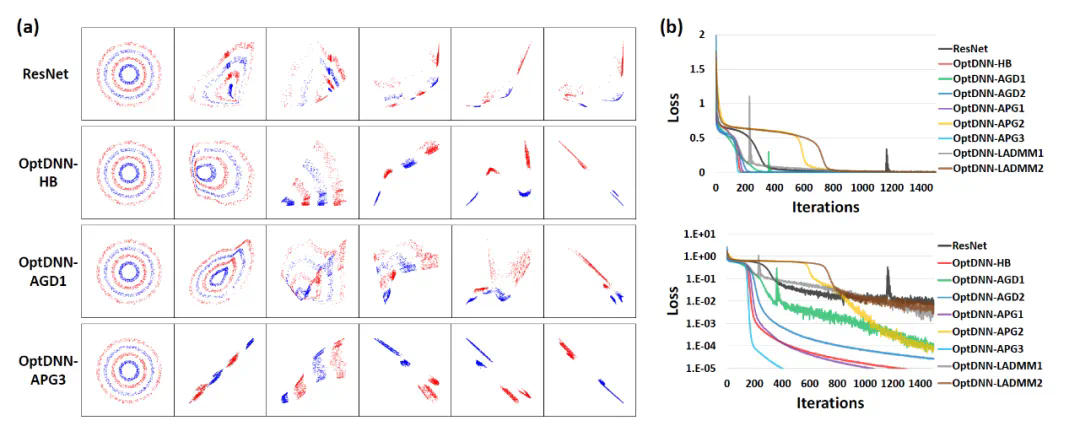
图 3 OptNN 逼近 parity function
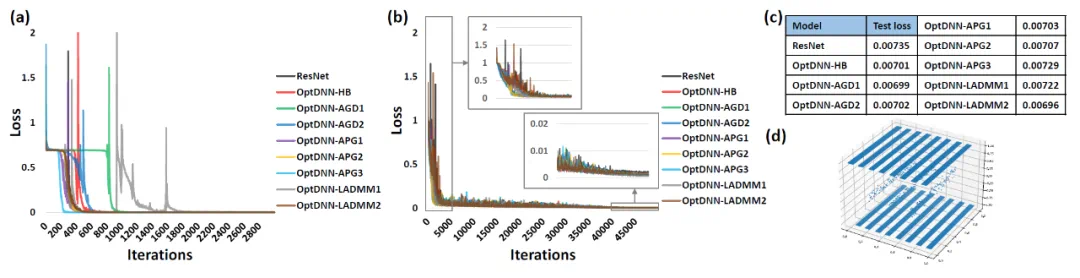
图 4 OptNN 逼近 Talgarsky function
然后,OptDNN 分别在宽 – 浅和窄 – 深两种设定下在 CIFAR 数据集上进行了图像分类任务的实验,结果见表 3 与 4。实验均在较强的数据增强设定下进行,可以看出,一些 OptDNN 在相同甚至更小的 FLOPs 开销下取得了比 ResNet 更小的错误率。论文还在 ResNet 和 DenseNet 设定下进行了实验,也取得了类似的实验结果。
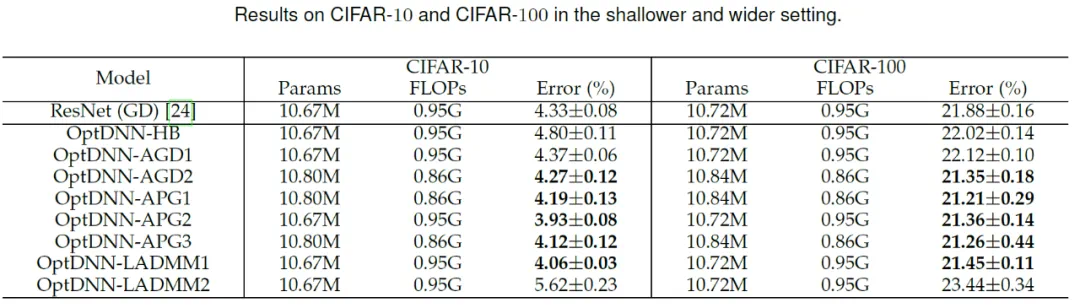
表 3 OptDNN 在宽 – 浅设定下的实验结果
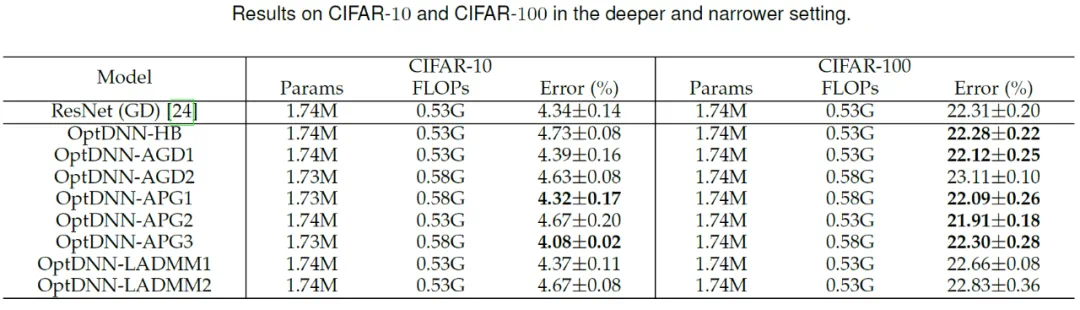
表 4 OptDNN 在窄 – 深设定下的实验结果
论文进一步选取了此前表现较好的 OptDNN-APG2 网络,进一步在 ConvNext 和 ViT 的设定下在 ImageNet 数据集上进行了实验,OptDNN-APG2 的网络结构见图 5,实验结果表 5、6。OptDNN-APG2 取得了超过等宽 ConvNext、ViT 的准确率,进一步验证了该架构设计方法的可靠性。

图 5 OptDNN-APG2 的网络结构

表 5 OptDNN-APG2 在 ImageNet 上的性能比较
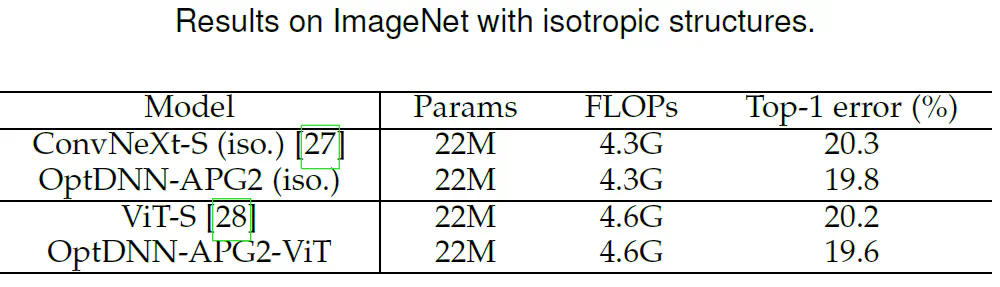
表 6 OptDNN-APG2 与等宽(isotropic)的 ConvNeXt 和 ViT 的性能比较
最后,论文依照 Proximal Gradient Descent 和 FISTA 等算法设计了 3 个隐式网络,并在 CIFAR 数据集上和显式的 ResNet 以及一些常用的隐式网络进行了比较,实验结果见表 7。三个隐式网络均取得了与先进隐式网络相当的实验结果,也说明了方法的灵活性。
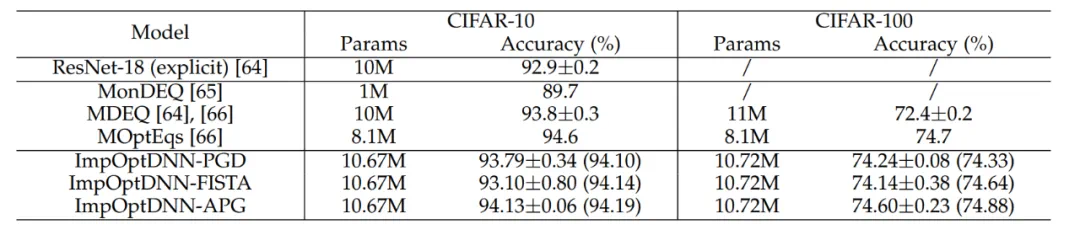
表 7 隐式网络的性能比较
总结
神经网络架构设计是深度学习中的核心问题之一。论文提出了一个利用一阶优化算法设计具有万有逼近性质保障的神经网络架构的统一框架,拓展了基于优化设计网络架构范式的方法。该方法可以与现有大部分聚焦网络模块的架构设计方法相结合,可以在几乎不增加计算量的情况下设计出高效的模型。在理论方面,论文证明了收敛的优化算法诱导的网路架构在温和条件下即具有万有逼近性质,并弥合了 NODE 和具有一般跨层连接网络的表示能力。该方法还有望与 NAS、 SNN 架构设计等领域结合,以设计更高效的网络架构。
参考文献
[1] B. Baker, O. Gupta, N. Naik, and R. Raskar, “Designing neural network architectures using reinforcement learning,” in International Conference on Learning Representations, 2017.
[2] V. Monga, Y. Li, and Y. C. Eldar, “Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing,” IEEE Signal Processing Magazine, 2021.
[3] K. Hornik, M. Stinchcombe, and H. White, “Multilayer feedforward networks are universal approximators,” Neural Networks, 1989.
[4] K. Gregor and Y. LeCun, “Learning fast approximations of sparse coding,” in International Conference on Machine Learning, 2010.
[5] S. Bai, J. Z. Kolter, and V. Koltun, “Deep equilibrium models,” in Advances in Neural Information Processing Systems, 2019.
[6] Q. Li, T. Lin, and Z. Shen, “Deep learning via dynamical systems: An approximation perspective,” Journal of the European Mathematical Society, 2022.





