共计 4186 个字符,预计需要花费 11 分钟才能阅读完成。
AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com。
从国际顶流 GPT-4 128K、Claude 200K 到国内「当红炸子鸡」支持 200 万字上下文的 Kimi Chat,大语言模型(LLM)在长上下文技术上不约而同地卷起来了。当全世界最聪明的头脑都在卷一件事的时候,这件事的重要性和难度就自然不言自明。
极长的上下文可以极大拓展大模型的生产力价值。随着 AI 的普及,用户已经不再满足于调戏大模型几个脑筋急转弯,用户开始渴望利用大模型来真正提高生产力。毕竟从前花一周憋出来的 PPT,现在只需要喂给大模型一串提示词和几份参考文档就分分钟生成出来,打工人谁能不爱呢?
新型高效序列建模方法比如:Lightning Attention (TransNormerLLM), State Space Modeling (Mamba), Linear RNN (RWKV, HGRN, Griffin) 等最近成为炙手可热的研究方向。研究人员渴望通过改造已经 7 岁高龄的 Transformer 架构,获得性能与之旗鼓相当,但复杂度仅为线性的新型架构。这类方法专注于模型架构设计,并提供了基于 CUDA 或 Triton 的硬件友好实现,使其能够像 FlashAttention 一样在单卡 GPU 内部高效计算。
与此同时,另一个长序列训练的杀手锏:序列并行获得了越来越多的关注。通过把长序列在序列维度切分为多个等分短序列,再将短序列分散至不同 GPU 卡并行训练,再辅以卡间通信便达到了序列并行训练的效果。从最早出现的 Colossal-AI 序列并行、到 Megatron 序列并行、再到 DeepSpeed Ulysses、以及近期的 Ring Attention,研究人员不断设计更加优雅高效的通信机制以提升序列并行的训练效率。当然这些已知方法全部是为传统注意力机制设计的,本文中我们称之为 Softmax Attention。这些方法也已经有各路大神做了精彩分析,本文不过多探讨。
那么问题来了。如何让新型高效序列建模方法实现序列并行,从而跨越单卡 GPU 显存限制实现真正意义的无限序列长度(当然你得有无限 GPU)的高效大语言模型训练,成为了一个开放的问题。已经成熟的序列并行方法如 DeepSpeed Ulysses, Megatron-SP 当然可以应用在线性序列建模方法上,但以 Softmax Attention 为设计蓝本的它们注定天生不是最优解。

本文即将介绍的 LASP 便应运而生。来自上海人工智能实验室的研究人员提出了 Linear Attention Sequence Parallelism (LASP) 方法以充分利用 Linear Attention 的线性右乘特性实现高效的序列并行计算。在 128 卡 A100 80G GPU、TransNormerLLM 1B 模型、FSDP backend 的配置下,LASP 可以最高将序列长度扩展至 4096K,即 4M。与成熟的序列并行方法相比,LASP 可训练的最长序列长度是 Megatron-SP 的 8 倍、DeepSpeed Ulysses 的 4 倍,速度则分别快了 136% 和 38%。
值得注意的是,虽然方法的名字包含 Linear Attention,LASP 并不局限于 Linear Attention 方法,而是可以广泛应用于包括 Lightning Attention (TransNormerLLM), State Space Modeling (Mamba), Linear RNN (RWKV, HGRN, Griffin) 等在内的线性序列建模方法。

LASP 方法介绍
为了充分理解 LASP 的思路,让我们先回顾下传统 Softmax Attention 的计算公式:O=softmax ((QK^T)⊙M) V,其 Q, K, V, M, O 分别为 Query, Key, Value, Mask 和 Output 矩阵,这里的 M 在单向任务(如 GPT)中是一个下三角的全 1 矩阵,在双向任务(如 BERT)中则可以忽略,即双向任务没有 Mask 矩阵。我们下面将 LASP 拆为四点进行解释:
Linear Attention 原理
Linear Attention 可以视为 Softmax Attention 一种变体。Linear Attention 去除了计算成本高昂的 Softmax 算子,Attention 的计算公式可以写为 O=((QK^T)⊙M) V 的简洁形式。但由于单向任务中 Mask 矩阵 M 的存在,使得该形式依然只能进行左乘计算(即先计算 QK^T),从而不能获得 O (N) 的线性复杂度。但对于双向任务,由于没有 Mask 矩阵的存在,其计算公式可以进一步简化为 O=(QK^T) V。Linear Attention 的巧妙之处在于,仅仅利用简单的矩阵乘法结合律,其计算公式就可以进一步转化为:O=Q (K^T V),这种计算形式被称之为右乘,可见 Linear Attention 在这种双向任务中可以达到诱人的 O (N) 复杂度!

LASP 数据分发
LASP 首先将长序列数据从序列维度切分为多个等分的子序列,再将子序列分散发送至序列并行通信组内的所有 GPU,使得每张 GPU 上各有一段子序列,以供后续序列并行的计算使用。

LASP 核心机制
随着 decoder-only 的类 GPT 形式的模型逐渐成为 LLM 的事实标准,LASP 的设计充分考虑了单向 Casual 任务的场景。由切分后子序列 Xi 计算而来的便是按照序列维度切分的 Qi, Ki, Vi,每一个索引 i 对应一个 Chunk 和一个 Device(即一张 GPU)。由于 Mask 矩阵的存在,LASP 作者巧妙地将各个 Chunk 对应的 Qi, Ki, Vi 区分为两种,即:Intra-Chunk 和 Inter-Chunk。其中 Intra-Chunk 为 Mask 矩阵分块后对角线上的 Chunk,可以认为仍然有 Mask 矩阵的存在,依然需要使用左乘;Inter-Chunk 则为 Mask 矩阵非对角线上的 Chunk,可以认为没有 Mask 矩阵的存在,可以使用右乘;显然,当切分的 Chunk 越多时,对角线上的 Chunk 占比越少,非对角线上的 Chunk 占比越多,可以利用右乘实现线性复杂度 Attention 计算的 Chunk 就越多。其中,对于右乘的 Inter-Chunk 的计算,前向计算时每个设备需要使用点对点通信 Recive 上一个设备的 KV,并 Send 自己的更新后的 KV 给下一个设备。反向计算时则正好相反,只是 Send 和 Recive 的对象变为了 KV 的梯度 dKV。其中前向计算过程如下图所示:

LASP 代码实现
为了提高 LASP 在 GPU 上的计算效率,作者对 Intra-Chunk 和 Inter-Chunk 的计算分别进行了 Kernel Fusion,并将 KV 和 dKV 的更新计算也融合到了 Intra-Chunk 和 Inter-Chunk 计算中。另外,为了在反向传播过程中避免重新计算激活 KV,作者选择在前向传播计算后立即将其存储在 GPU 的 HBM 中。在随后的反向传播过程中,LASP 直接访问 KV 以供使用。需要注意的是,存储在 HBM 中的 KV 大小为 d x d,完全不受序列长度 N 的影响。当输入序列长度 N 较大时,KV 的内存占用变得微不足道。在单张 GPU 内部,作者实现了由 Triton 实现的 Lightning Attention 以减少 HBM 和 SRAM 之间的 IO 开销,从而加速单卡 Linear Attention 计算。
想要了解更多细节的读者,可以阅读论文中的 Algorithm 2(LASP 前向过程)和 Algorithm 3(LASP 反向过程),以及文中详细的推导过程。
通信量分析
LASP 算法中需要注意前向传播需要在每个 Linear Attention 模块层进行 KV 激活的通信。通信量为 Bd^2/h,其中 B 是 batch 大小,h 是头数。相比之下,Megatron-SP 在每个 Transformer 层中的两个 Layer Norm 层之后分别使用了一次 All-Gather 操作,并在 Attention 和 FFN 层之后分别使用了一次 Reduce-Scatter 操作,这导致其通信量为 2BNd + 4BNd/T,其中 T 为序列并行维度。DeepSpeed-Ulysses 使用了 All-to-All 集合通信操作来处理每个 Attention 模块层的输入 Q, K, V 和输出 O,导致通信量为 4BNd/T。三者的通信量对比如下表所示。其中 d/h 是头维度,通常设置为 128。在实际应用中,当 N/T>=32 时,LASP 便能够实现最低的理论通信量。此外,LASP 的通信量不受序列长度 N 或子序列长度 C 的影响,这对于跨大型 GPU 集群的极长序列并行计算是一个巨大的优势。

Data-Sequence 混合并行
数据并行(即 Batch-level 的数据切分)已经是分布式训练的常规操作,在原始数据并行(PyTorch DDP)的基础上,已经进化出了更节省显存的切片式数据并行,从最初的 DeepSpeed ZeRO 系列到 PyTorch 官方支持的 FSDP,切片式数据并行已经足够成熟并被越来越多用户使用。LASP 作为 Sequence-level 的数据切分方法,可以能够和包括 PyTorch DDP, Zero-1/2/3, FSDP 在内的各种数据并行方法兼容使用。这对 LASP 的使用者来说无疑是好消息。
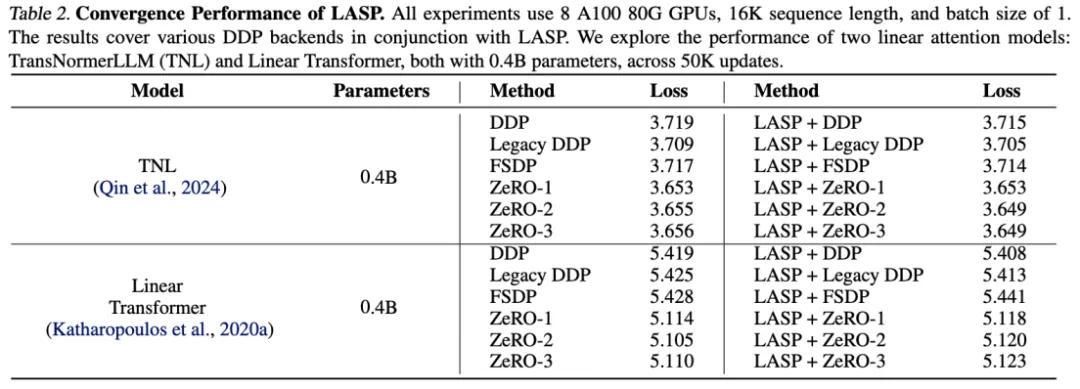
精度实验
在 TransNormerLLM (TNL) 和 Linear Transformer 上的实验结果表明,LASP 作为一种系统优化方法能够和各种 DDP backends 结合,并均能达到与 Baseline 持平的性能。
可扩展性实验
得益于高效的通信机制设计,LASP 可以轻松扩展至上百卡 GPU,并保持很好的可扩展性。

速度对比实验
与成熟的序列并行方法 Megatron-SP 和 DeepSpeed-Ulysses 对比,LASP 可训练的最长序列长度是 Megatron-SP 的 8 倍、DeepSpeed-Ulysses 的 4 倍,速度则分别快了 136% 和 38%。

结语
为了方便大家试用,作者已经提供了一个即装即用的 LASP 代码实现,无需下载数据集和模型,只需 PyTorch 分分钟体验 LASP 的极长极快序列并行能力。
代码传送门:





