共计 1838 个字符,预计需要花费 5 分钟才能阅读完成。
AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
过去十年间,基于随机梯度下降(SGD)的深度学习模型在许多领域都取得了极大的成功。与此同时各式各样的 SGD 替代品也如雨后春笋般涌现。在这些众多替代品中,Adam 及其变种最受追捧。无论是 SGD,还是 Adam,亦或是其他优化器,最核心的超参数非 Learning rate 莫属。因此如何调整好 Leanring rate 是炼丹师们从一开始就必学的技能。
从直觉上讲,影响 Learning rate 取值的重要因素是 Batch size。不知你在学习炼丹术时,是否遇到或者思考过入如下问题:
针对上述问题,腾讯混元联合北京大学基于现有科研基础和实际业务需求,在进行了大量理论分析和实验验证后发布了关于 Batch size 和 Learning rate 放缩关系的调参指南:

1. 当使用 SGD 风格的优化器时,应当采用 OpenAI 2018 年给出的结论():
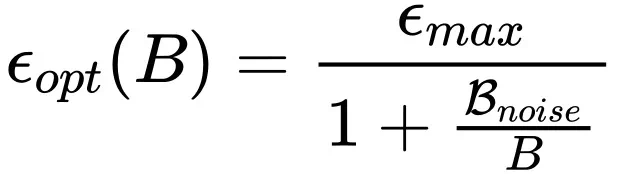
2. 但是当使用 Adam 风格的优化器时,需要按照如下放缩规律:
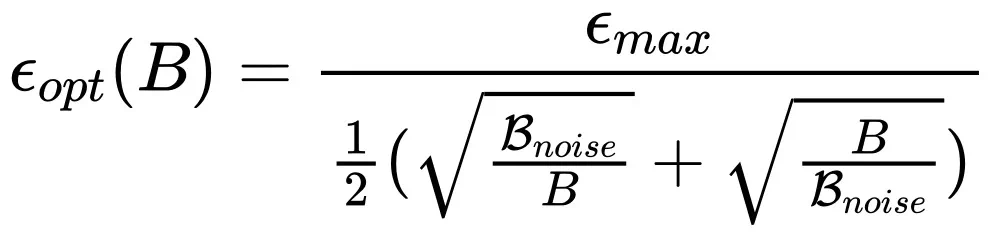
其中
和 B 分别代表 Learning rate 和 Batch size,而

与 OpenAI 2020 年 Scaling law 论文()中的
对应。从上面结论不难发现,当
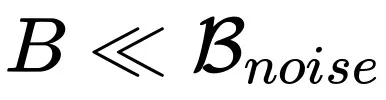
时,社区中广为流传的线性放缩和平方根放缩在一定范围内都是正确的,并且分别对应使用 SGD 风格和 Adam 风格优化器的情况。
一、居然要降低学习率?
如果仔细观察 Adam 风格优化器放缩规律的表达式子会发现,当 Batch size 超过

后,随着 Batch size 增加最优的 Learning rate 反而是下降的!这样的结论似乎有点反常,但是仔细思考之后又觉得是合理的。首先我们回顾一下 Adam 的更新形式,梯度的一阶动量除以二阶动量的平方根:

(更详细的讨论参考原文中的附录 A)。与 SGD 直接采用 G 进行参数更新相比,

将更快的进入饱和区间,例如,假设 G 的均值是正实数,随着 Batch size 增加
估计为正数时,再增加估计的准确度对

的结果也毫无影响了。因此当 Batch size 超过

时,增加的信息不足以抵消

带来的噪声影响,从而导致此次的更新不再那么确信,以至于需要降低学习率。
二、观察到的下降区间
为了检验理论的正确性,需要从实验中观察到最优学习率的 “下降区间”。既然从上一节的分析中发现,使用 Adam 优化器时 Batch size 超过

就会导致最优学习率下降,那么只要确定出

取值,然后在通过网格搜索打点观察就可以了。虽然从形式上

计算很困难,但是幸运的是基于 OpenAI 关算于训练时间和样本效率的定量结论中我们可以估算出
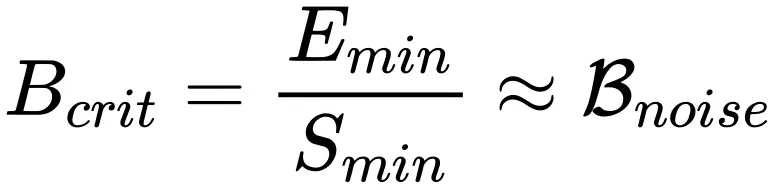
的取值(更详细的讨论参考原文中的附录 G)。
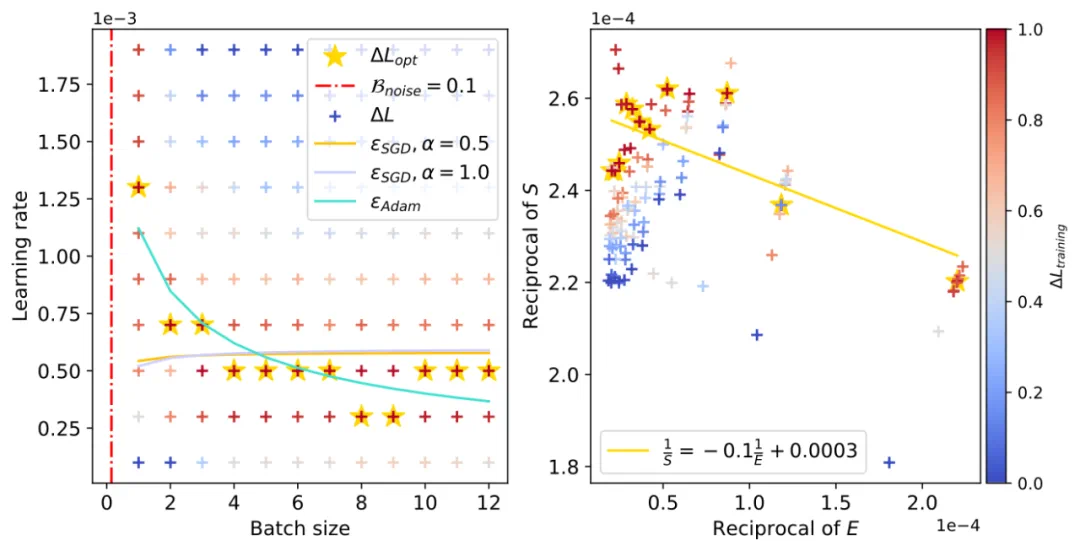
上面展示了 CNN 在 FashionMNIST 上的学习率 “下降区间”。左图为通过 OpenAI 定量公式估算的
(左图直线斜率的负数,右图红色竖直虚线),右图中黄色五角星代表不同 Batch size 下的最优 Learning rate 取值,青色实线为我们的理论预估曲线。

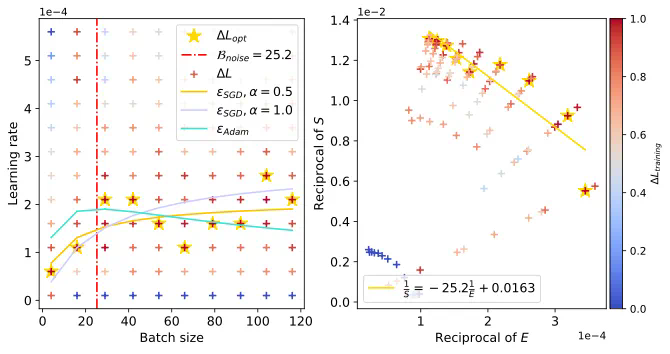
以及 Resnet18 在 TinyImagenet,和 DistilGPT2 在 Eli5Category 上也观察到了类似现象。
三、浪涌现象
前面我们从理论和实验上都发现了,在使用 Adam 风格优化器时最优学习率曲线就像一朵 “浪花” 一样随着 Batch size 增加会先升高后下降。同时结合 OpenAI scaling law 的结论,随着训练进行

会逐渐变大。我们理论预测并实验证明了随着训练进行 “浪花” 逐渐向着大 Batch size 方向涌动:
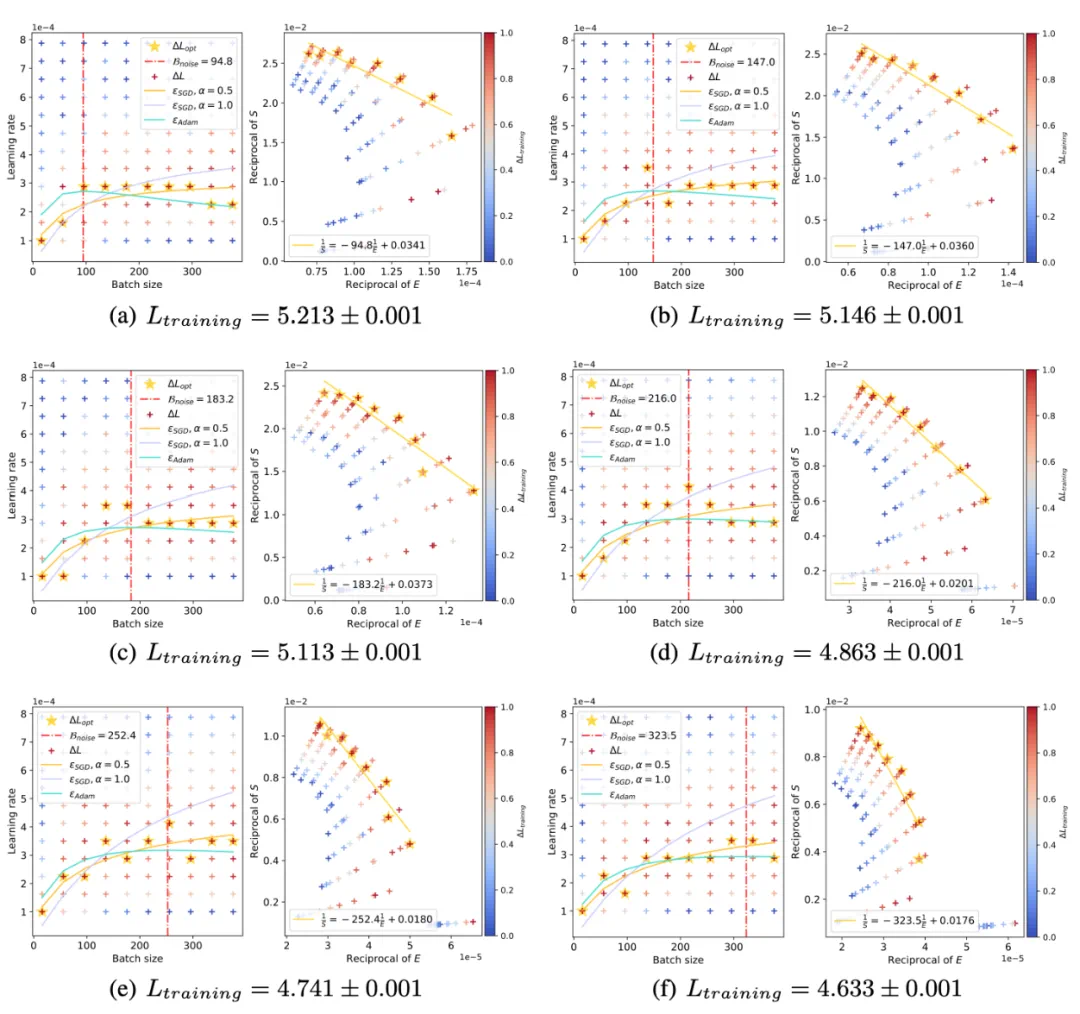
四、理论发现
前面讨论过 Adam 风格的优化器在进行参数更新时采用类似
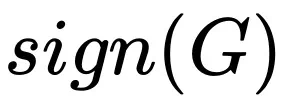
的形式。虽然此形式看起来很简单,但是由于推导过程涉及到对更新量均值和方差的考量,所以我们在处理的时候做了一个假设和一个近似:
1. 假设每个样本的参数 i 的梯度服从均值为

,方差为
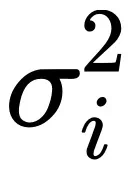
的高斯分布
2. 通过 sigmoid-style 函数对高斯误差函数进行数值近似
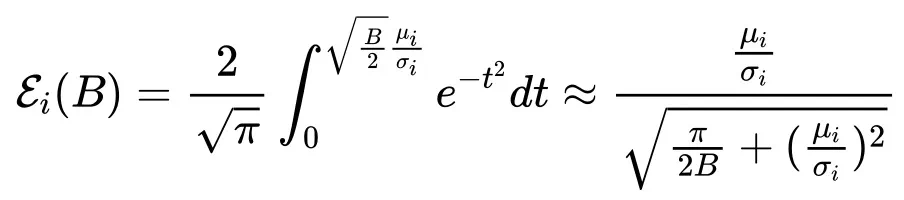
当
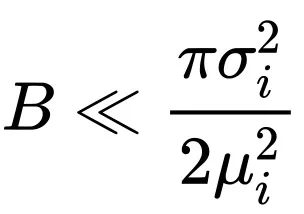
时,完整的 Scaling law 形式近似为:
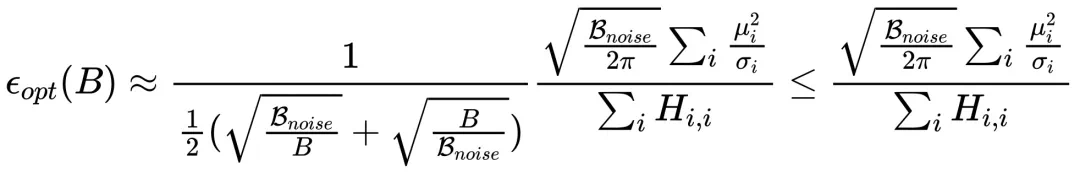
其中
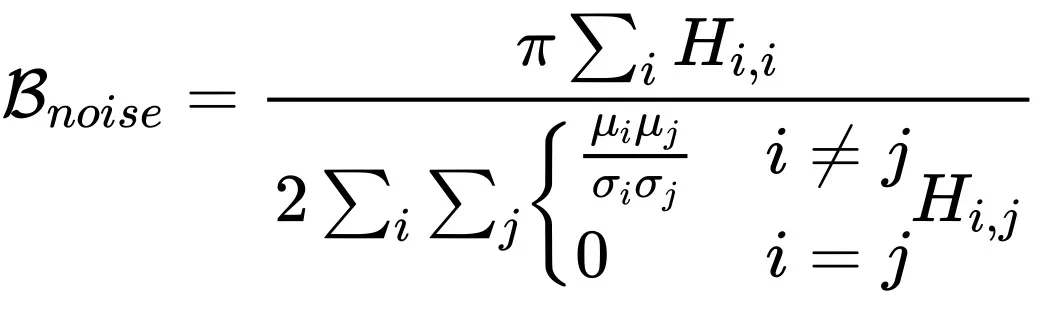
,H 为海森矩阵。
当
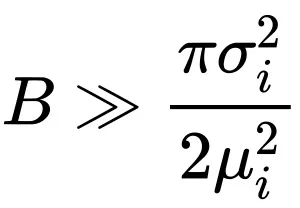
时:
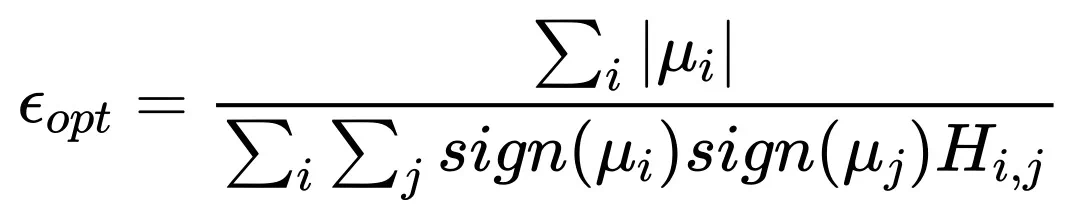
表明,Batch size 无限大时最优学习率趋于一个饱和值。
五、应用
我们在腾讯 Angel 大模型训练框架中集成了上述理论成果,并在腾讯混元大模型训练任务中对理论进行进一步验证,未来将服务于各种大模型训练场景。
感谢阅读,更多详细内容,请参考原文。





